| Home > Spudguns > Spudgun Physics |
| Home > Spudguns > Spudgun Physics |
OK. So you knew that at some point there would be at least some science in this. And this page is its home. In case you haven't already noticed, there is actually a lot of physics in one little spudgun. In fact, there are hundereds of calculations that could be performed. This page is limited to a few of the more interesting ones, such as distance, speed and explosive force. But first a warning: yes, there is math in this. Because math is evil, I have tried to keep it clear and to a minimum. Most of it is just multiplying, dividing and subtracting, although there is a small amount of trigonometry. Nothing that can't be solved with the aid of a calculator. So, here goes...
What we are interested in calculating is the speed of the potato, the distance straight up, and the average explosive force. First, though, we will need to shoot the spudgun and take some measurements. You will need two observers apart from each other at a fixed and known distance. 20M is is a good choice. Those observers will use inclinometers to measure their angle to the spud when it reaches the apex of its arc. It should look something like the diagram below.
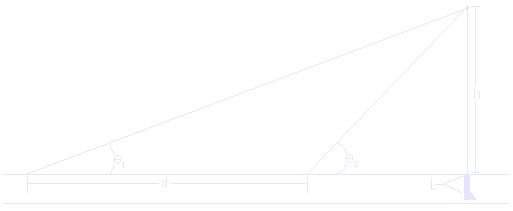
The potato is shot straight up into the air. The observers track the spud with their inclinometers and record the angle at which the potato stops in mid air. It will hang there for a split second at it's maximum height. The first angle is Theta 1 (on the diagram as a Theta with a subscript one on the right), the second is Theta 2 (same as one, just with a two). These angles will hence forth be refered to as "Angle 1" or "Angle 2" in the text, but will remain as Theta 1 or 2 in the equations. Anyway, aside from angles 1 and 2, you will also need to know the mass of the potato in kilograms and the length of your spudgun barrel in meters. Note that this is the mass after it is shot, because the sides get trimmed off as it is shoved into the barrel.
For this example, lets assume that angle 1 is 65 degrees, angle two is 55 degrees, the mass of the potato is 0.05 kilograms, the length of the barrel is 0.92 meters, and the distance between the observers is 23 meters. We would then use the equation as below to get the height of the shot.

Note that the result has been rounded to three decimal places. This makes it easier to work with, but a little less accurate. Our remaining calculations will be a little off, but for purposes of example this should not matter. If you are doing this in real life, you would want to use the memory feature of your calculator.
Once we have the the height, we can go about calculating the muzzle velocity. You will note a strange "9.8" that appears in the equation, seemingly out of nowhere. This is actually a constant representing Earth's gravity. This number would have to be adjusted if you were shooting on the Moon or Mars.
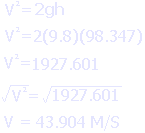
And we get an approximate (remember, things have been rounded) value of 43.904 meters per second. Once we have this figure, average force in Newtons is easy to calculate, as shown below. That 0.05 is the mass of the potato, the 9.8 is the Earth's gravity (or rather, acceleration due to gravity) and the 98.347 is of course the height. The whole thing is divided by the length of your spudgun barrel in meters.
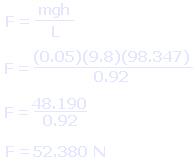
Now wasn't that easy?
If you want to do the same for your spudgun, you can simply measure the required angles, lengths and masses, then plug the numbers into the form below.